Task #1

The first task asks students to make a function that models profit per hour, taking into account the $10 of bus fare. In addition to being a relevant context that will help you answer the inevitable question of “When am I ever going to use this in ‘real life’?”, this task highlights two features of Woot Math Polls, equivalence and custom legends of common responses. The short answer task is designed to accept multiple versions of any correct answer. If your students write f(x)=-10+15x they will still get it right; the same goes for y=15x-10 and y+10=15x. We even allow scaled versions of the equation, although it would be unlikely that a student would write 2y=30x-20, though they would still get it right. If you want to change any of the equivalence options, simply open the task and click on the gear icon, the following menu will appear:

If you don’t want to accept y in place of f(x) you can deselect it. If you don’t want to accept X in place of x (we recommend not making it case sensitive since some keyboards automatically capitalize) you can select the “Match Case” option. Scaling lets you accept larger and smaller versions of equivalent equations.
The prompt asks for the function to be written as f(x) but we decided to allow y as well for correct answers since if the student is getting this close, they are doing the math right and can get feedback later on which form to put it in. But wouldn’t providing this feedback be tedious and hard to scale to my 30+ students?
I’m glad you asked. That’s where the custom legend comes in. Student responses are automatically categorized based on a custom legend that can be tailored to each problem. This task has the following custom legend:
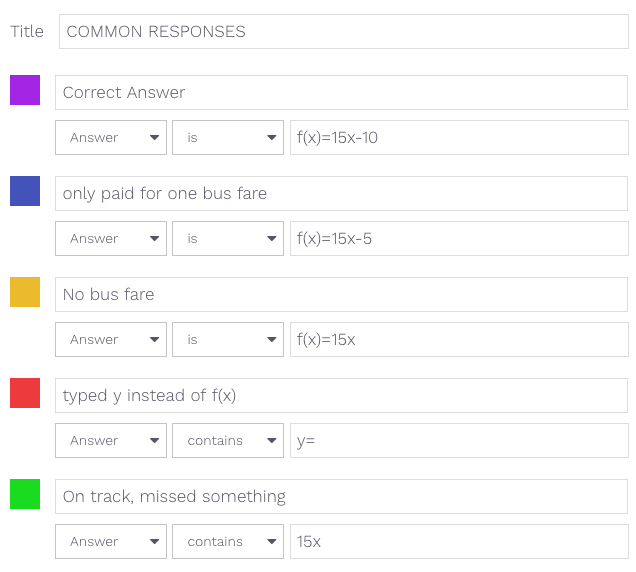
The custom legend looks from the top down so it is important to have the correct answer first. If they did not account for the return bus fare, their response will show up blue on your dashboard. If you want them to have feedback about f(x) vs y without telling them they are wrong you can see who typed y in their answer (regardless of if they were correct) and remind them to pay attention to the prompt. If you want to praise students for getting close by correctly modeling the rate, you can see those responses in green. By automatically categorizing your responses, this task helps you provide more nuanced feedback and move your students learning forward.
The next task has students model the same relationship but as a function of total hours, h instead of hours worked, x. In this case, h=x+2 so replacing x with h-2 will get you the correct answer.

But wait! Isn’t f(h)=15h-40 equal to f(h)=15(h-2)-10? Yup! That’s why this task has no assigned correct answer. After students respond you can display the results and have them discuss (in groups if you want) what they all think the correct answer is. Also, if students finish early, you can ask them to find the other correct answer as a challenge. This task also provides an opportunity to review equivalence and distribution.

In the third task, students model an old job where they made a commission of 20 per sale plus $10 per hour but are maxed out at $100 per day. This task, when combined with the next one gives them more opportunities to work on modeling and also adds some variables that take value judgements and let them connect their own out of class experiences. How hard is it to sell a bike? If you sold a lot, would it be worth it to go home early? How many hours a day do you want to work?
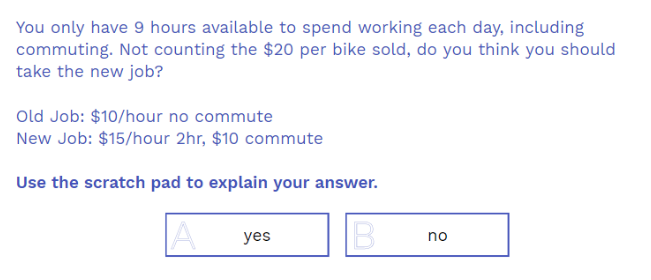
The final task has them compute the convergence point of the two jobs. This gives them more data to address the question of if they should take the new job or not. There is no correct answer but you can expect student responses to pull in topics ranging from how many hours they want to work, if they like bus rides or not, if they had a car or carpooled if it would be shorter, and if they value having a higher wage more than convenience.
We encourage you to modify this task and content to align it with similar content. You can copy the poll and modify or delete any task and also make new ones. Please reach out with any questions or comments, we’re here to support you!
Get started by previewing the poll right now, or login to wootmath.com and search for the New Job poll in the Shared Gallery.