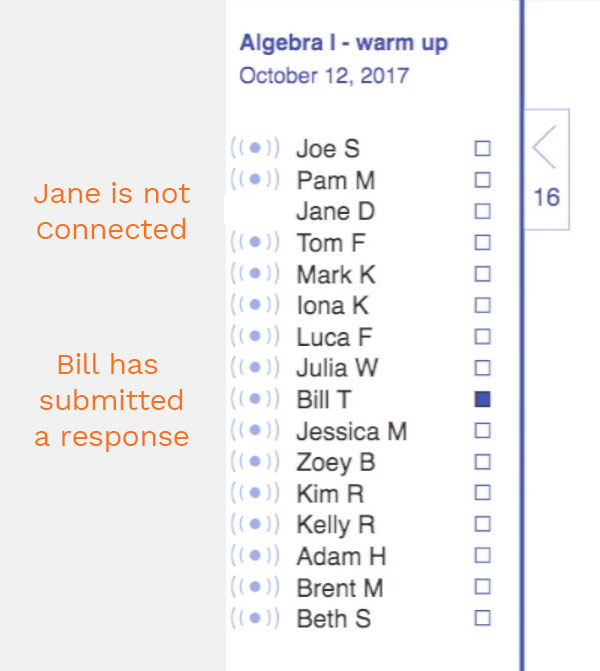
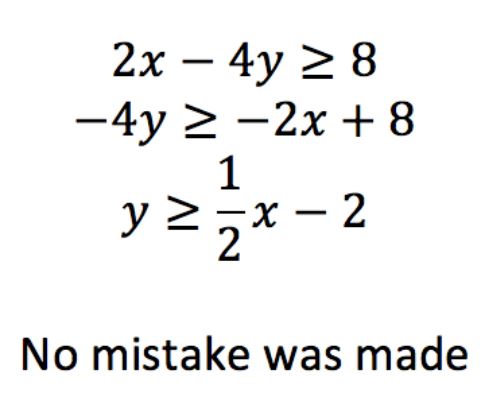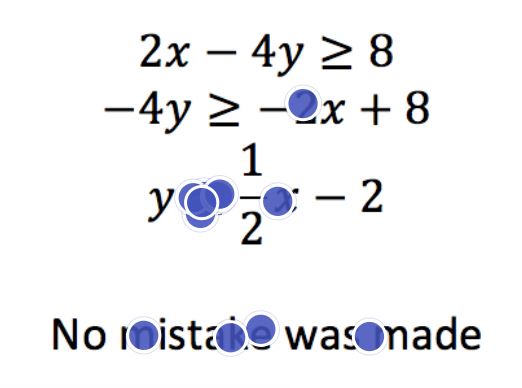Posted on

Answer key for the formative assessment questions?

I would like to run one of the formative assessments (quiz, exit ticket, warm up, etc) for my classroom. Is there an answer key somewhere? Can I change the answers?

There are a number of ways to explore a problem set before assigning it to your students. This FAQ will address some of the more common ways that teachers explore the existing content from the problem bank.

Preview

An easy way to run a formative assessment is to preview it. To preview questions, hover over the tile in the content and press preview. Then you can play through it.

When you preview it, then you will see what the student will see. You can also answer the questions to ensure that you are happy with the set responses.

Modify an Answer

If you would like to modify an answer, remove or add additional problems, or make any other changes, you can also do that. First hover over the tile in the content and press Copy.

This will make a copy and place it in My Content. Then you can edit it to review the answers, change the questions, etc.

From the edit page, you can see all of the questions, add/remove items, etc.

To edit a particular question, press the pencil icon. This will take you to the creation interface, where you can change answers, how the question is written, etc.  You can use the Next Task / Preview Task to quickly navigate through the questions.

One common question teachers have are units – what units are expected. Since many of these formative assessments are created by teachers, and the expectations vary based on district, school, teacher, and grade, it is always advisable to play through it prior to providing it to your students. And if necessary, you can make changes to the problem so that your students will not be confused.

Posted on

Make Your Virtual Classroom Interactive with Woot Math’s Teacher-Led Activities

How to Use Woot Math with Video Conferencing

Make Your Virtual Classroom Interactive with Woot Math’s Teacher-Led Activities

Did you know that you can use Woot Math’s Teacher-Led activities and any video conferencing application to run an interactive and engaging virtual classroom? With the following tips, you can have face-to-face interaction, and share student work in real time for great discussions.
The Coronavirus is causing many (if not all) schools to close for normal operations. Distance learning is suddenly a necessity and teachers are scrambling for activities that they can assign to their classes and still have productive learning going on. But not all distance learning needs to be independent. By carefully planning a lesson with Woot Math’s formative assessment platform, you can have an engaging and productive discussion with your students.

Plan Carefully

Learning new software can be difficult. Be sure to practice operating your video conferencing software so that you are comfortable with it, and know how to share your screen or browser window, and how to cancel sharing. With a bit of preparation, you can avoid accidentally sharing the wrong window with your entire class!

Sometimes you may want your students to be focused on their work in their device’s window of Woot Math, and sometimes you will want them focused on your shared screen in the video conferencing app. Of course, sometimes you will just want the class to be together, seeing each other and interacting without any shared screen.

Use The New Slide Task for Instructional Content

You can create any lecture-style material you want to cover by inserting a “Slide” task into your unit, and then modifying the scratchpad. This can be anything you can create on the scratchpad with our digital tools, or you can upload an image or PDF as the content as well. If you already have your content prepared, you can upload it directly to a new slide by selecting Import Worksheet, below the new task type selector. When projected, the slide content will display on your screen and the students’ devices so that they can see clearly what you are talking about.

Slide task

Monitoring Student Engagement

There are several ways you can make sure your students are paying attention with Woot Math. The left-hand panel will display who is connected to the platform (the little wifi icon), as well as who has successfully submitted a response to the current task (a solid blue square next to their name).

Left panel

You can also use the live view of student work to see what they are doing on their scratchpads in real time. Just be sure to not share your screen when you look, or you will share that student’s work with everyone in the class. Read this blog post to learn more about live view.

Live View of Student Work

Class Discussion

Once the students have completed their work and submitted their answers, share your Woot Math screen with the class. Select Display Work, and you can review your students’ work with the class to help drive discussions, reveal common misunderstandings, and help keep everyone connected.

Display Student Work
To open a student’s answer and scratchpad, just click on any of the tiles. The X in the upper right corner will let you close it again when you are ready to move on to another example.
Student work open for review

This is a challenging time for all of us. We hope this approach may be useful for you and your students. If you have any questions or suggestions, please contact us. We are here to help.

Stay safe and stay well.

Visit our page on Formative Assessment for more on how to use this free tool in your classroom.

Woot Math
All Posts »
Posted on

Live View of In-Progress Student Work

Live View of Student Work

Live View of In-Progress Student Work

An exciting new feature just launched to help teachers monitor students’ work in real time with “Live View.” Live View gives teachers the opportunity to see what students are working on, without having to look over a student’s shoulder. Sounds great, right? Let’s dive into how it works.

Live View is available in any “Teacher-Led” activity. To get started, launch a teacher-led activity. Once the activity has begun, at the bottom of the screen there will be an arrow to pop up the “Real Time Student Work.” You have the option of displaying student names or not.

Live View Tab
To avoid accidentally displaying student work for the whole class to see, please follow the tip and freeze your projector screen before opening up the “Live View”. Remember, most projector remotes have a ‘freeze’ button that locks what it is projecting at that moment.

After clicking, “Got It!” a view of each students’ workspace will show on your screen. Scroll down to view all of the students’ work.

This view offers teachers lots of information about how the class is doing on each task. The border color indicates student progress: blue (not yet started), yellow (partially correct), red (incorrect) and green (correct). The border color changes dynamically while the student is working on the task. The color of the title bars show whether the student has submitted their response and if it is correct (green), incorrect (red), or not submitted (blue).

For example, in the screenshot below, we see that Jaden has answered correctly (and pressed submit), Alice has input the correct answer (but has not yet pressed submit), Jose has answered incorrectly (also not yet pressed submit), and Marc has not yet worked on the problem.

Live View of Student Work

This tool makes it easier to find students who need some extra support or help during work time.

Live View is also great for finding exemplars or common misconceptions to review with the class after submissions. We love how Woot helps teachers create a culture of learning from common mistakes, this tool makes that process even more efficient. After you find some student work you want to review, click the bookmark button to pull it up later. We have found that when reviewing student work, it’s good to focus on what the student did well, and what they can do to improve. A mix of praise and feedback helps with confidence and keeps students motivated to improve. Also, bookmarks are anonymous to help avoid social pressures around sharing work.

bookmark Exemplar Student Work
Seeing student work in real-time is a great formative assessment tool, allowing you to tailor your instruction based on students’ current needs and understanding. You can quickly review what everyone in the class is doing, all in real time! In addition to helping you give support during work time, this feature supports teachers in finding pieces of student work to highlight when reviewing the task. Exemplars and common mistakes are great ways to communicate expectations to students, leveraging the power of Woot Math.

We hope you enjoy Live View and please don’t hesitate to reach out with success stories, questions, tips or questions.

Visit our page on Formative Assessment for more on how to use this free tool in your classroom.

woot-master
All Posts »
Posted on

New Tie Breaker Feature in Team Mode Promotes Positive Interdependence

Tie Breaker screenshot

New Tie Breaker Feature in Team Mode Promotes Positive Interdependence

Since Woot Math launched Team Mode in the fall, students, more than ever, have been loving collaborating with their peers to solve problems. If you haven’t tried out Team Mode in your classroom, check out the New Team Mode for Collaborative Learning blog post to learn more.

This week we launched a new feature to provide teachers the opportunity to encourage students to work and collaborate to make sure everyone on the team knows how to solve the problem. Teachers can now award half points to teams who do a great job showing their work. This incentive encourages students to engage in the activity and show their best work. Also, it helps break ties at the end of team mode. Let’s jump right into how it works.

How it works

Part of what makes Woot Math great is the ability for students to show their thinking on the scratchpad. We’ve added a way for you to reward great work, and tied it into Team Mode’s scoring. You’ll find a new button on the Team Mode leaderboard, “Bonus for Great Work”:
Team Mode Leader Board

This view anonymously shows samples of each team’s work. It’s up to you to determine which team(s) should be awarded a ½ point bonus for showing great work. Or you can use this as an opportunity to award partial credit to a team that’s demonstrated a good effort, but didn’t quite get to the correct answer. If multiple teams show excellent work, feel free to award as many teams as you wish with the bonus. When finished, click “Done” to see the fun animated results on the leaderboard. Those teams receiving the bonus will see a gold star next to their avatar for that round.

Great Work Bonus Screen

Positive Interdependence

This feature arose out of requests for more ways to support teachers as they promote positive interdependence during group work. Groups work best when everyone is engaged, participating and working together.

Positive Interdependence has two components. Positive correlation of outcomes and student dependence on one another for success. When students do well, their team does well. When they just copy the answer and don’t engage with the problem, they bring the group down. The group outcomes are positively correlated to the individuals outcomes. Also, the group should have incentive to depend on one another. When you help your peers understand how to solve a problem, the team does better.

Team mode already promotes interdependence since everyone in the team needs to have the right answer to get the point. The bonus point feature takes this a step farther, not only does everyone need to have the right answer, they need to show how to solve the problem…no more relying on that one teammate who knows the right answer. Now students have more incentive to work together to make sure everyone on the team understands the mathematics. Instead of pinning students against one another, Woot Math is getting students to work together on teams to be instructional resources for one another.

This new feature also supports teachers as they work to create a culture in the classroom where students work together. A teacher doesn’t have to use the ‘great work button’ often, just enough so students know they are accountable and need to show work for their team to be successful.

Tie Breaker

On the last question of the poll, in the event of a tie for first place, a tie-breaker button will show up. You’ll be able to select a winner based on the quality of work shown on that final question.
Tie Breaker screenshot
When you click the “Start the Tie Breaker” button, it works just like the “Great Work Bonus” from previous questions. Except now it only shows the teams tied for first place, and you can break the tie with a Great Work Gold Star!
Tie Breaker Detail
Make your selection, click done, and the winner is revealed!
Team Mode Winner Screen
We hope that you enjoy this new feature and find your students excited and motivated to show great work as they work collaboratively to solve rich tasks in Woot Math Team Mode.

We hope you enjoy team mode and please don’t hesitate to reach out with success stories, questions, tips or questions.

Visit our page on Formative Assessment for more on how to use this free tool in your classroom.

Woot Math
All Posts »
Posted on

New Team Mode for Collaborative Learning

Moving Team Members Around

New Team Mode for Collaborative Learning

Students have access to more technology for learning than ever before. It’s in their backpacks, classrooms, computer labs… even their pockets!

Despite all the improvements in learning technology over the last decade, computers are not the most powerful asset in a math classroom. By having your students work with their peers, you can leverage the most powerful tool in the room… the human brain in each of your students. When they work together in team mode, students explain, listen, argue, justify and question. They also tend to have more fun. As far as technology has come, students still have more fun working on math with friends than with a computer. 

Here at Woot Math, we believe in the power of collaborative learning and the power of educational technology. That’s why we are excited to introduce Team Mode. This new feature groups students on teams, facilitating collaboration on engaging, rich math tasks. Students work together with their team but still have individual accountability to showing work and understanding the solution, not just copying answers. Team Mode is part of Woot Math’s free Formative Assessment platform and comes to you, free, with no strings attached. “How does it work?” “Get me started!” “Yes please!” We hear you. Read on to learn more.

Getting Started with Team Mode for Collaborative Learning

There are two ways to start team mode. Both involve finding some content either from your content or our library of free, public content. Click “teacher led” to launch the Woot. The simple way to start Team Mode is to click the team mode button before you launch.
Starting Team Mode

By selecting Team Mode, you are opting to run the entire Woot with students in teams. If you want to start with individual mode and switch to Team Mode part way through, Woot can do that too. You can switch to Team Mode at any time by clicking on the hamburger menu in the upper right corner and selecting Team Mode. This will make the rest of the activity run in Team Mode

Starting Team Mode Option 2

The next step is for you to put your students into teams.

Make Groups How You Want, or How They Want

First, you decide the group size, making teams from 2 to 8 students. In our testing, we found teams of 3-4 are the sweet spot but the choice is yours. You also pick how the groups are made. The groups can be made at random or picked by students. If you started Team Mode in the middle of a Woot, you can also have the software make the teams heterogeneously based on correctness of the last question. That way, you get mixed teams with some students who got the last one right and some who needed a little extra help. You can also make homogenous teams. We recommend this after a fun question asking about what hobbies they have or what kind of shows they like to watch. 

“What if I don’t like the teams it made?” Great question! 

The teacher has final say over the teams, just drag a team member to a new team or put them on another team. We know that sometimes there are classroom dynamics where it is best to have some students not work with certain others or some students to work with someone in particular… the choice is yours. Below, we see a teacher moving Jeff off of team Shark, to team Cricket and then replacing him with Jefferson.

Moving Team Members Around

How Does The Scoring Work?

Now that you have started team mode, students will work together to solve problems. The team earns a point if everyone gets the correct answer. If just one student is incorrect, the team does not earn a point. Note that everyone does not need the same answer, they just need a correct answer. Woot Math has tools that allow tasks to accept equivalent answers as correct.
This scoring method promotes collaborative learning since the success of the team depends on the success of each individual. Make sure you still hold students accountable to showing their work, this is another great way to make sure everyone is engaging with the problem, not just copying answers.

Individual Work Time Before They Collaborate

Team Mode problems start with individual work time before students collaborate. In our testing, we found that students have more to talk about and collaborate more evenly if they have some time to work on their own before collaborating. Each task starts with a two minute timer where students can’t submit until the timer is done, feel free to add or remove time as you see fit. We found that this solo time really pays off.

Practice Math Facts While You Wait for Others to Finish

Want your students to stay engaged while they wait for others to finish? We thought so.

Woot Math now has a math facts game for them to play while they wait for their peers to finish. Students solve math fact problems and work on improving their recall and fluency.

Engaging math game between problems

We have found that the game is just fun enough to keep (most of) them off youtube but not so fun that they rush through the real task to get to the game.

If you want a fun way to get your students used to team mode and the functionality of the scratchpad, check out Team Mode Orientation, a warm up that we made to help get your students used to Woot Math. To preview the activity, click the link, or login to wootmath.com and search for “Team Mode Orientation” in the Shared Gallery.

We hope you enjoy team mode and please don’t hesitate to reach out with success stories, questions, tips or questions.

Visit our page on Formative Assessment for more on how to use this free tool in your classroom.

Woot Math
All Posts »
Posted on

Differentiated Formative Assessments

Differentiated Formative Assessments

Do some of your students finish early while others struggle to start the problem? If you’re a teacher then the answer is probably, YES!

We have teamed up with some of our teacher partners to help support teachers with the age old task of differentiation. We co-designed formative assessments to support learners of any pace. Look for the tag #differentiated to find these assessments. They incorporate language supports, bonus problems and hints. Best of all, there are custom legends to identify if a student is emerging, demonstrating or exceeding in their fluency of a standard.

Sometimes students struggle to answer math problems because of the language demands, not the math content. We don’t want these students to miss out. We also want to make sure they can participate in doing the classroom math. This is where language supports and sentence starters come in. If a task asks students to explain their thinking, a sentence starter will help get them going on the mathematically juicy part of the sentence without having to worry about all of the writing demands.

tap an image prompt

– Tap an Image Prompt –

For the above task, students need to identify where on the line represents the greatest velocity and then explain their thinking. Some students will have trouble getting started with the writing so we included some sentence starters in the scratchpad.
sentence starters

– Sentence Starters –

Now, students can focus on the mathematics without getting bogged down in the writing. If you have learners who don’t need the sentence starters, encourage them start their sentences in other ways.

In addition to the challenge of writing, assessments can contain new vocabulary that trip students up. For example, a student may forget what velocity means. With the language support below, they get a gentle reminder that lets them focus on relating the graph to the motion of an object. This makes the assessment about the math instead of their vocabulary.

– Velocity Language Supports –

As the teacher, you can remove any of these supports that don’t fit your class. Simply go to scratchpad settings and tap the text box , then press the orange x. Remember to click “save” when you are done.

While some need extra support, other students will be ready to demonstrate mastery of the standard.  Thus, #differentiated polls have bonus problems in select tasks. Bonus problems in the scratchpad relate to similar content to the original task. For example, the tap an image task from above has the following bonus problem.

Example of a Bonus Prompt
– An Example Bonus Problem –

The bonus problem above goes beyond the comparative nature of the task. It asks students to find the slope of the line when it has the greatest velocity.

Bonus problems also work to assess if students understand the greater context of the problem. Reviewing answers and student responses can ignite productive discussion for everyone. For example, a different bonus problem asks students to write a story, including units, that corresponds to the graph.

– Write a Story Bonus Problem –

The discussion about the responses to this bonus problem will be informative to everyone.  On the next task, all students are asked to pick between potential stories for a similar graph.

distance from home problem
– Distance From Home Problem –

Hearing their peers share how stories connect to the previous graph makes the pathway for success more clear to all students. Search #differentiated in the explore content tab or follow one of the links below to get started with differentiated tasks. Or create your own! 

Visit our page on Formative Assessment for more on how to use these strategies in your classroom.

Woot Math
All Posts »
Posted on

New Feature: Active Learning Through Student Volunteers

New Feature: Active Learning Through Student Volunteers

Woot Math has a new feature to help you promote active learning during formative assessment activities in your classroom. You might be thinking, “Wait...doesn’t Woot Math already do that?”. That’s right. Students have always been able to show their work during formative assessments. Now, they can also volunteer to present their work or have the teacher use their work as an exemplar.

Ask for Volunteers

Student work is always saved when running a formative assessment. After students complete the task, in teacher-led mode teachers can review examples of anonymous student work in real-time with the class. Now, the teacher can also ask for volunteers by clicking on the volunteers tab. Once they do, students can now volunteer to share their work with the class.

Students can volunteer

– Students Can Volunteer to Show Their Work –

Select High Quality Student Work

Once students have volunteered, the teacher sees tiles from each of the student volunteers. The teacher can then determine which student volunteer they want to project by simply clicking on the tile.

Teacher sees a list work from student volunteers

– Teacher Sees Work From Student Volunteers –

For this problem, Joelle and Aaron have volunteered their solutions. The green check box indicates that they both have the correct answer. The teacher can turn off revealing the correct answer by deselecting “reveal answer”. Sometimes it is helpful to project student work without the answer revealed – students can then use critical thinking and analytical skills when they have to justify their responses before being told if they are correct.

Promote Active Learning: Have Students Present Their Work

To promote active learning, the teacher can select one of the volunteers to explain their solution. In this case, it appears that Joelle has shown more extensive work than Aaron. Work for this blog post comes from the activity called Pythagoras’ Park. Students apply their understanding of the Pythagorean Theorem to story problems about walking through a park. Check it out here.
Students engage in active learning through presenting their work and solutions

– Projected Volunteer Student's Worked Solution –

We see that Joelle has used the Pythagorean Theorem to solve the question. She also remembered to find the positive and negative solutions to 25=c². This attention to detail makes it a great opportunity for active learning. Joelle can present her thinking to the class while other students can learn from her example. Of course, the teacher can also use this feature to present students’ work on their behalf.

This is a great feature to try out if you are looking to get your students more engaged in active learning. You can also use this feature to encourage students to take risks. Reassure them that it is good to share their thinking, even if they aren’t 100% correct yet.

We recommend you check out the Pythagoras’ Park activity as a review of they Pythagorean Theorem. It would also work well as a quick refresher for students who have already learned it! Previewing the activity now using the link below. Or, login to wootmath.com and search for “Pythagoras” in the Shared Gallery.

Preview Pythagoreas’ Park

Visit our page on Formative Assessment for more on how to use this free tool in your classroom.

Woot Math
All Posts »
Posted on

Scratchpad Tutorial: Assess Student Work

This week we talk about a fun new activity that walks you through the features of the scratchpad. This activity orients students to some of the great features of Woot Math for Formative Assessment. Showing your work is important in math and so is formative assessment. With Woot Math you collect and assess student work it digitally saving you time and getting them doing great work! 

It covers content up through fractions, computing radicals, knowing what pi is and computing exponents, all of which is normally covered by 8th grade, sometimes sooner. So if your students haven’t encountered them yet you can make a quick alteration to the activity and it should work for earlier middle-school students.

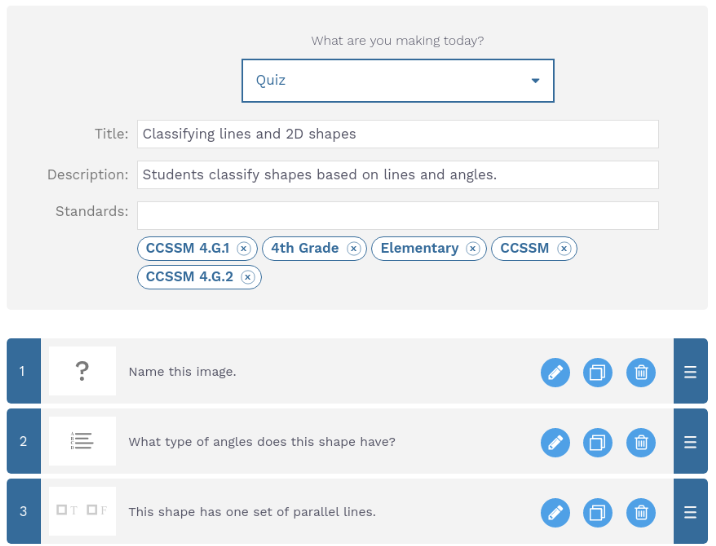
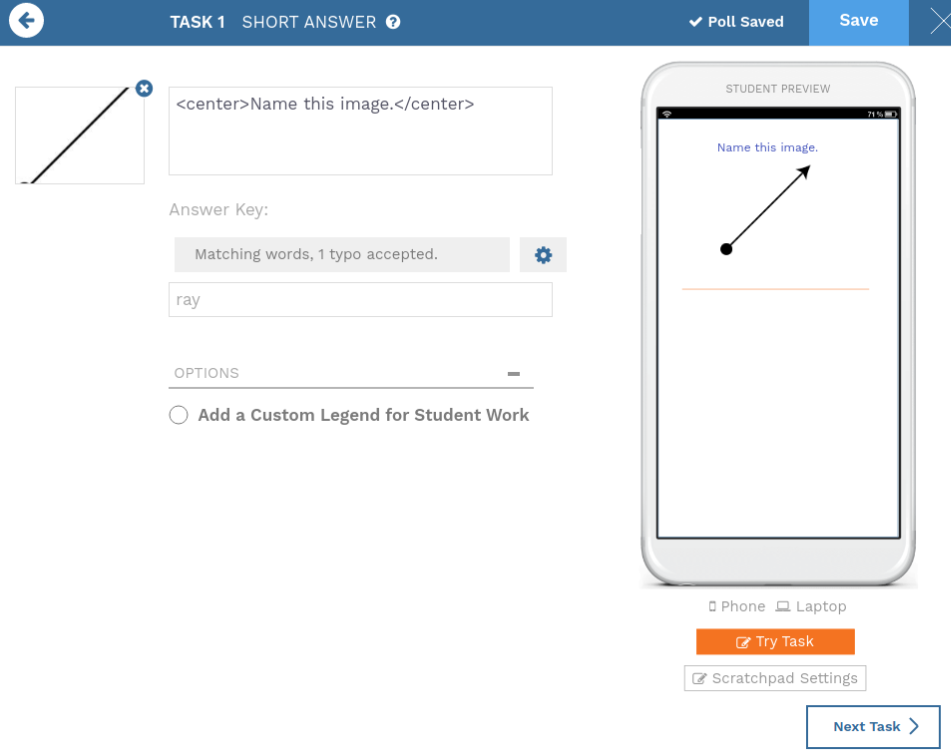
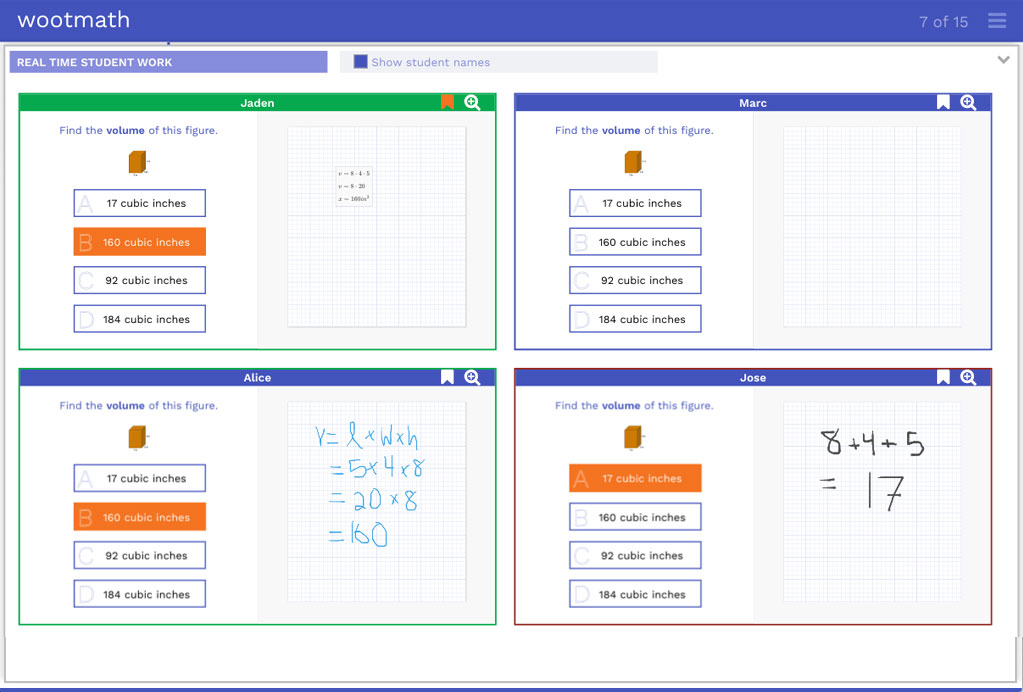
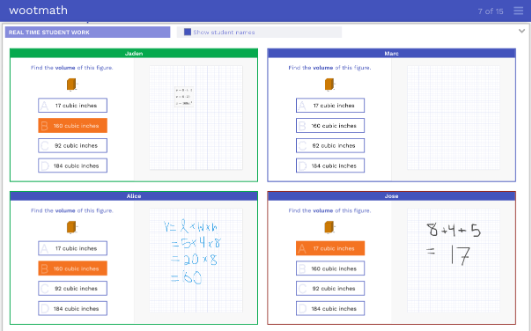
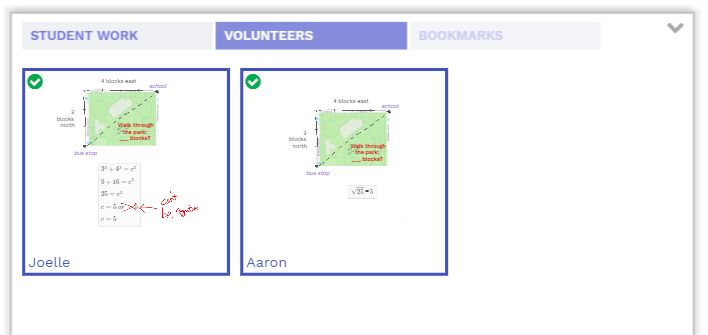
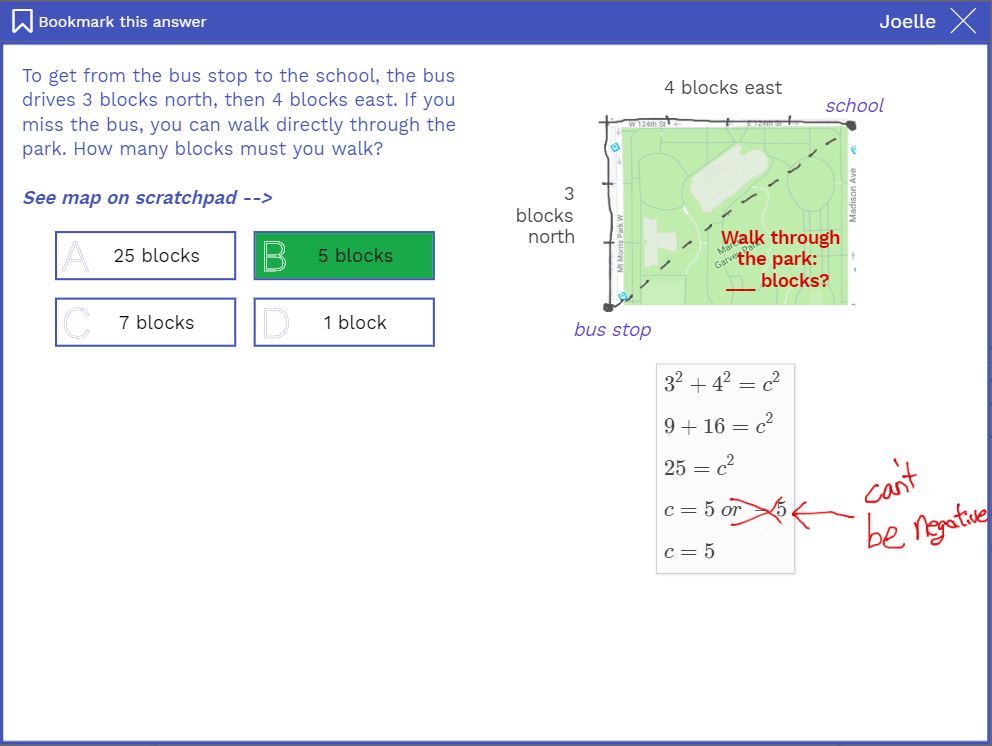
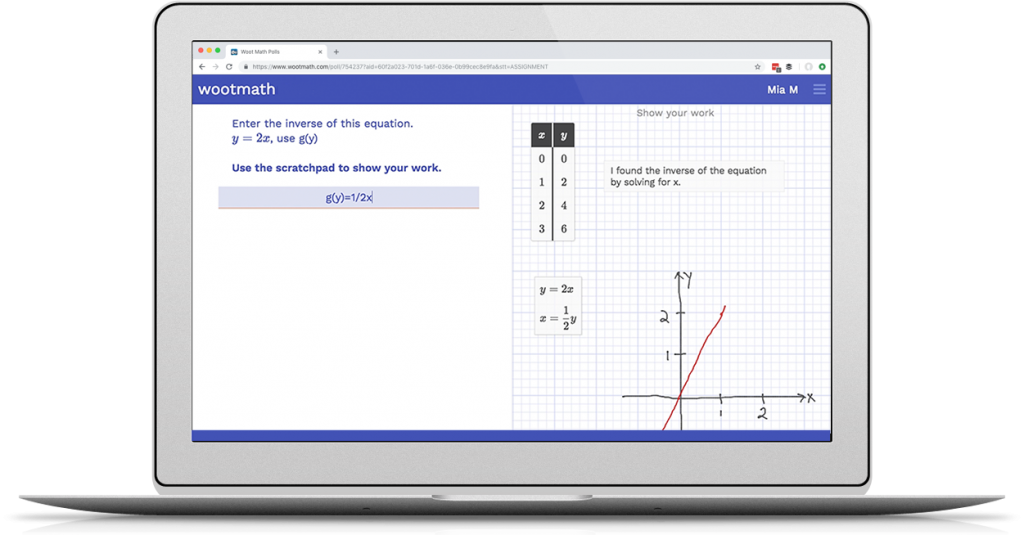
The first task asks students if the table feature can auto populate results (it can) and then to show their work. This little known feature of the scratchpad can be very helpful for students in using tables to support their work. If the first column has a variable (any letter) and the second column is an expression with that variable, it will automatically compute the values for you. Below is an example of some great work from a student on this task that you can access from the bookmarks tab:

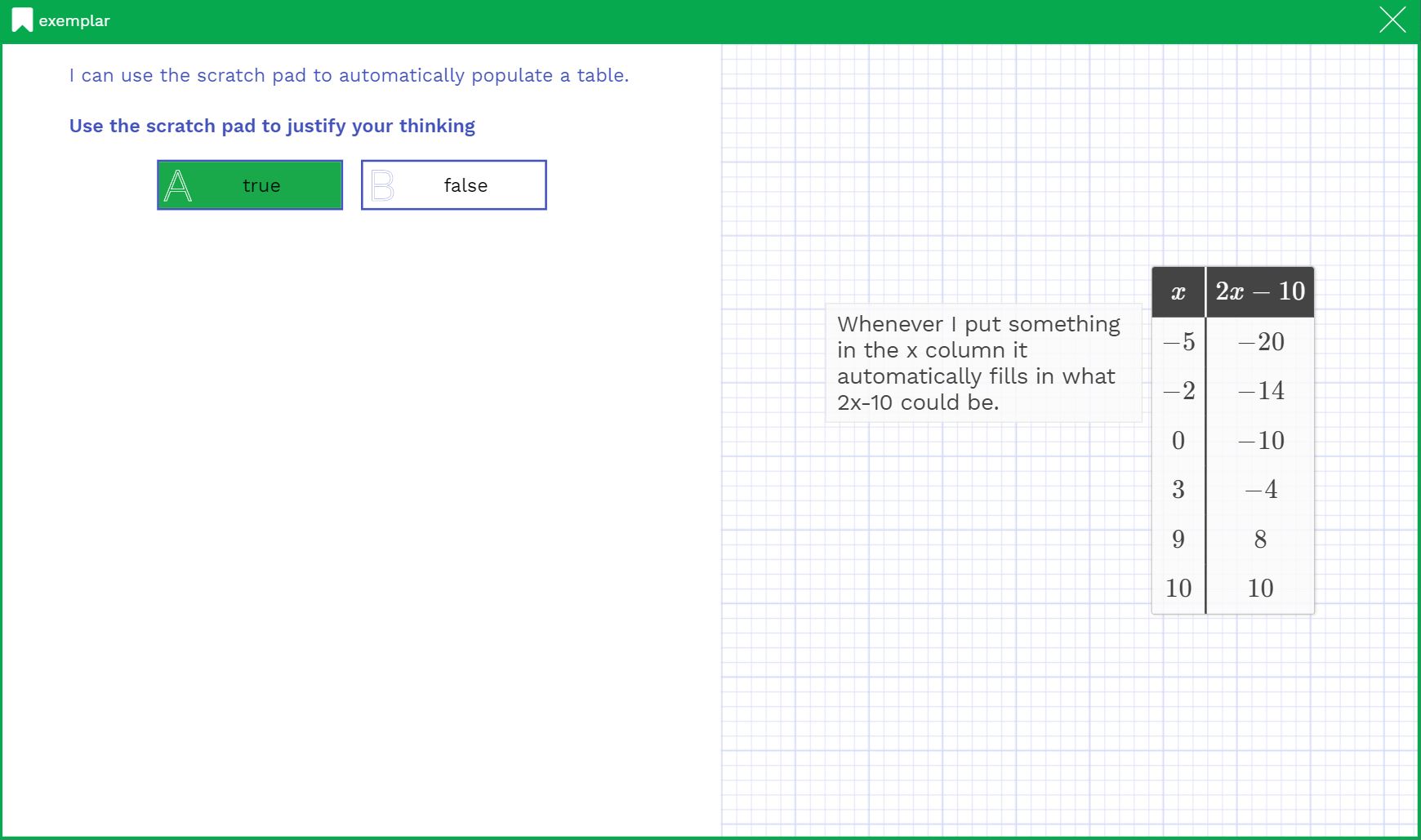
– Task 1: Example of Great Work –

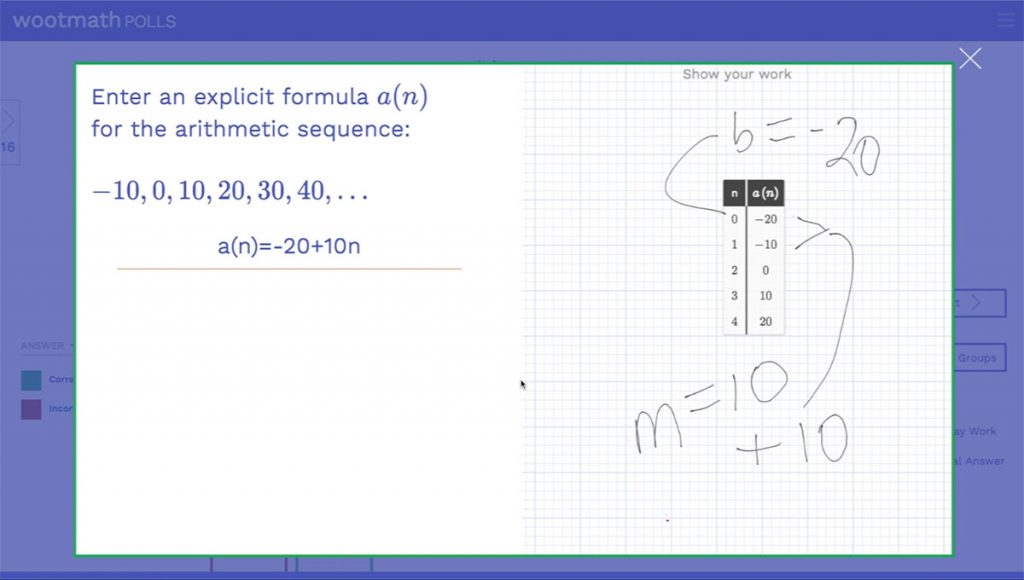
The next task asks students to write an equation on the scratchpad and then select how challenging they found it. The equation intentionally has all of the different components of the expression editor so they get practice with exponents, radicals, rational expressions and pi (typing pi and then space-bar gives you 𝝅).

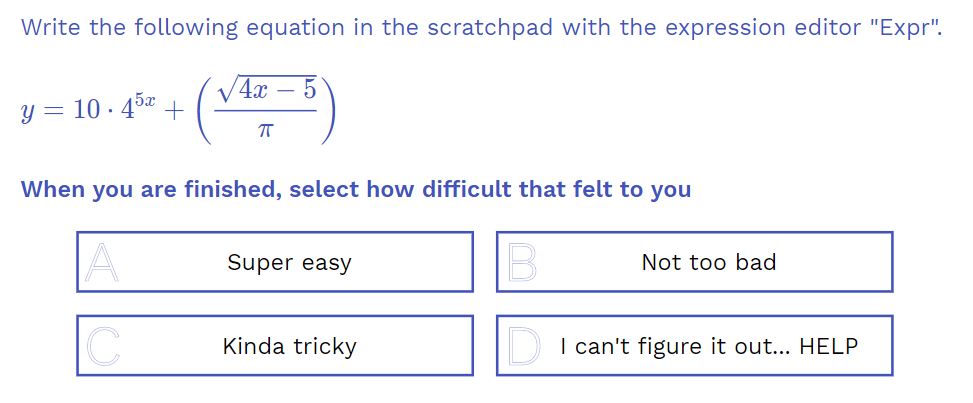
– Task 2: Writing an Equation on the Scratchpad –

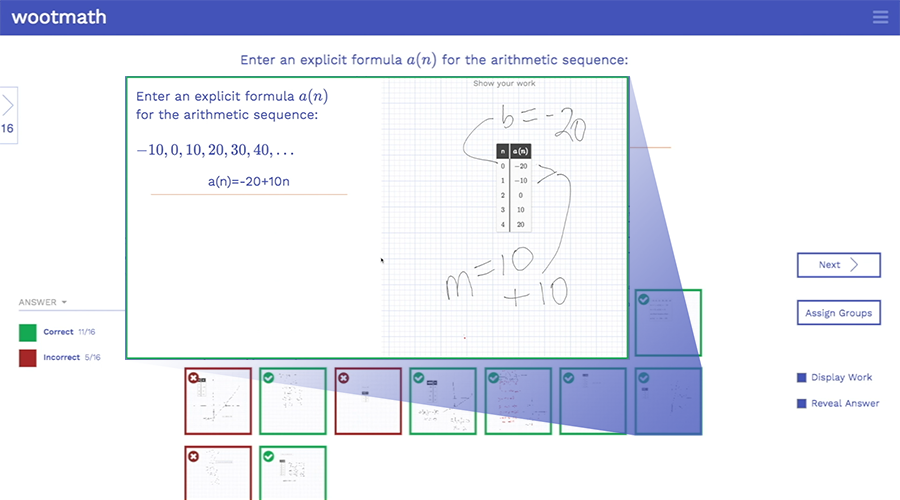
The results to this task will give you student responses to the multiple choice question but the custom legend is coded to see if they got the question right or not. Anyone coded purple wrote the correct equation on their scratchpad. The custom legend allows you to assess student work on the scratchpad as well as their responses. This gives you even more choices for how to design rich assessments.

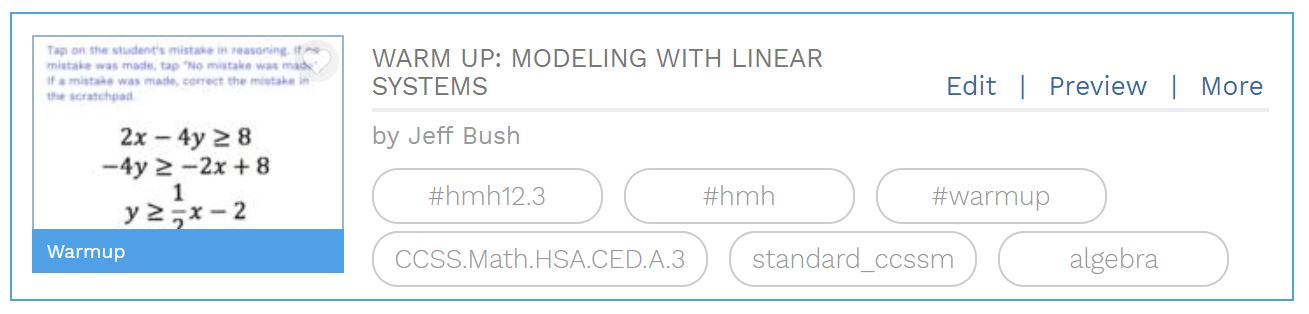
Task 3 has the students tap on the mistake in the projected problem and then solve it correctly in the scratchpad. This gives the students the choice of using the drawing tool, the text tool or the expression editor.

– Task 3: Tap the Mistake –

We recommend you suggest the text or expression editor if students are using a mouse or touchpad. For tablets, the drawing tool can be an efficient way to show your work.

The fourth and final task has students use the calculator on the scratchpad to compute the value of an expression. If students are having trouble with the calculator, encourage them to try the arrow keys on the calculator (or keyboard) to get the fractions to show up in different places. Parentheses also help if you are unsure about order of operations.

– Task 4: Scratchpad Calculator –

A fun tip: students can type s to write a square root, ^ to make an exponent, / to make a fraction and pi to make 𝝅. These notes are also in the scratchpad of this task as a support for students. Also, for a fun extension problem, you can ask them what other shortcuts they can find.

Analyzing student work lets you learn how students think about solving math problems. Having them show their work with these tools will help you learn how they are thinking and help you better conduct formative assessment.

Get started by previewing the activity right now, or login to wootmath.com and search for Scratchpad Tutorial in the Shared Gallery.

Preview the Activity

Visit our page on Formative Assessment for more information on implementing these strategies in your classroom.

Stay tuned for next week’s post!

Posted on

Math Misconceptions and Productive Discourse

Assessing Math Misconceptions

The first problem is a tap-on-the-mistake type. Students need to analyze the projected procedure and find the mistake (if there is one). Recognizing math misconceptions is a great exercise. 

Task 1 - Tap on the Mistake

– Task 1: Tap on the Mistake –

With tasks like this, everyone has the opportunity to do productive mathematics. If a student don’t know how to solve an inequality or where to start, they can evaluate the projected work. Everyone gets to apply their prior understandings of mathematics to this problem.
 
The fact is, your students might not catch this mistake. It is a subtle and often forgotten rule that dividing or multiplying an inequality by a negative requires flipping the inequality. If your students ask why this rule is true, you can tell them to think of it as multiplying each side by -1 and then dividing each side by 4. Inequalities are like unbalanced scales. One side is heavier than the other. When you multiply each side by -1, you are changing all negatives to positives and all positives to negatives, this means the scale will reverse. If one side weighed 10lbs and the other weighted 2 lbs the side with 10lbs is lower. Multiplying each side by -1 means the low side now weighs -10lbs (think of it as 10lbs worth of upward force from balloons). The other side is now -2lbs. 10lbs up will pull more than 2lbs so the side with 10lbs up is now higher. The scale has flipped so the inequality needs to flip.

Discussions about Math Misconceptions

Some of your students will likely choose the correct answer, and some will likely “choose no mistake was made”. Now is when the sneaky and magical power of Woot Math shines! Deselect the reveal answer button to reveal student responses as a heatmap without revealing who was correct.

– Uncheck Reveal Answer–

Some of your students might no think there is an answer, some (hopefully) got it right, and some may have chosen another place in the work. Those who got it wrong may have been guessing or may be going off of a juicy misconception… aka: a productive learning moment. For more on the value of learning from mistakes, check out Woot Math’s CEO, Krista Marks, Ed Surge article on Aha moments.

After you click show results, your heatmap might look a little something like this:

Task 1: Heatmap of Student Responses

– Task 1: Heatmap of Student Responses –

Small Group Discussions

This is a great opportunity for students to discuss the problem, either as a whole class or in small groups. You can ask the students to come to a consensus as a group. This is where another one of our favorite features comes in handy. With the “assign groups” button, Woot Math automatically groups of 2-6 students. You can choose to generate these groups based on if they put the same answer (homogeneous), a different answer (heterogeneous) or at random
Automatic Student Grouping

– Student Grouping –

With heterogeneous grouping by answer, each group should have someone who got it right (as long as you have enough students getting it right). Now, each of the groups is set up for success. Woot!

Get started by previewing the activity right now with the link below. Or, login to wootmath.com and search for Warm Up: Modeling with Linear Systems in the Shared Gallery.

Preview the Poll
Visit our page on formative assessment for more on how to use these strategies in your classroom.